|
|
|
|
|
|
|
This month's tips are all about transformations. We'll find
out how to reflect in a point, how to use reflections to create the
ideal path for a billiard ball, and, staying on the pool table, how to
use translations to quickly draw 15 pool palls racked up. We're on the web at www.mathillustrations.com. |
 Billiard Reflections
[Video] Billiard Reflections
[Video]
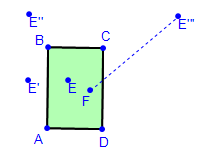
Given two balls on a billiard table, what path will take one ball to the other while first bouncing off 3 cushions? - Given
the two points E and F, and the table ABCD, reflect E in AB, then
reflect the image E' in a BC, then reflect its image E'' in CD.
- Draw a line segment connecting F with E'''. (make it dotted to distinguish it as a construction line).
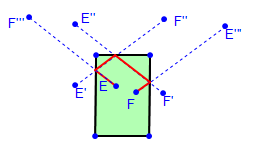 - Now reflect the line FE''' in CD, then reflect F'E'' in BC, then reflect F'''E in AB.
- Add new line segments which join E to F via the intersections between the construction lines and the sides of the table.
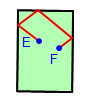
- Now you can hide the construction lines to leave only the ball's path.
For more reflection based models, look here , here and here . |
| |
Pool Translations
[Video]
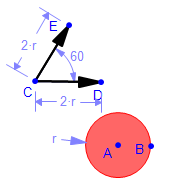 We'll use translations to create a picture of the triangular arrangement of pool balls at the start of a game.
- Draw a circle representing a ball. Specify its radius to be r.
- We
are going to create translated copies of this ball. We want to
translate either by distance 2r horizontally or at an angle of 60
degrees. So we create two vectors, one horizontal, and one at 60
de
 grees, and make the length of each 2*r. grees, and make the length of each 2*r. - Now
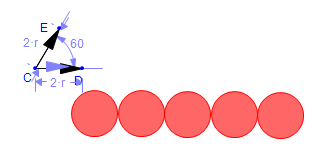
we translate the original ball using the horizontal vector, and repeat
translating the new ball till we have 5 balls arranged in a horizontal
line.
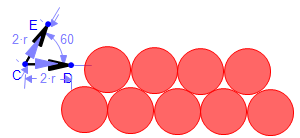
- Now we select the first 4 balls and translate using the diagonal vector.
- We repeat selecting 3 then 2 then 1 ball from the next 3 lines, eventually yielding the triangle of balls.
 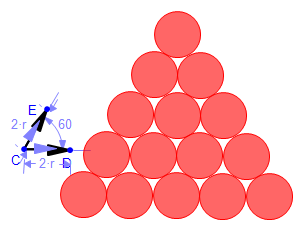
|
| |
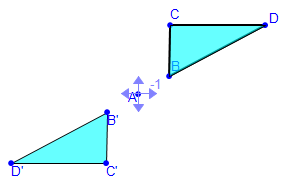
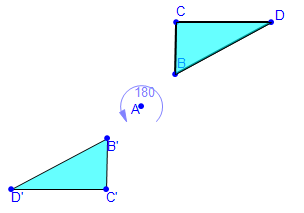
Point Reflections
Math Illustrations offers a full set of Euclidean transformations: translations, rotations, reflections, and dilations. But reflections are reflections in a line. What if you want to reflect an object in a point? There are two equivalent transformations which you can use to reflect in a point: - Rotate by 180 degrees about the point
- Dilate by a factor of -1 with a center at the point.
  |
| |
|
|
|